
Hi guys! It's Cherrie again, here to make another attempt to earn a badge, and to help my fellow students. Again, thanks to everyone who congratulated me, and thought my last scribe was great. Much appreciated :).
Today in class, Mr. K started us off with the following problems:
Find the related angle
a) 220°
a) 220°
b) 150°
c) 400°
Which, as a class, resulted in the answers:
a) 40°
b) 80°
and c) 40°
and c) 40°
How did we get to these answers, you ask? You're probably wondering what the related angle of an angle is. The related angle is the smallest angle made with the x-axis. As an example, I'll show you how we got to the answer for letter a.
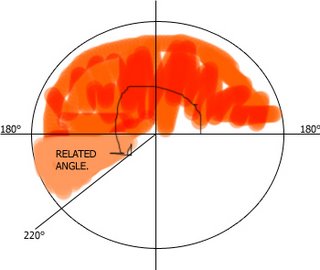 On the x-axis we have the landmark of 180°. If you start from the right, where it's marked 180°, and if we were able to measure accurately, 220° would approximately appear where I've marked it, so basically, the orange shaded region is 220°.
On the x-axis we have the landmark of 180°. If you start from the right, where it's marked 180°, and if we were able to measure accurately, 220° would approximately appear where I've marked it, so basically, the orange shaded region is 220°.The peach shaded region, is what we call the related angle, because just like the explaination said, it's the smallest angle made with the x-axis.
Now how we got the 40° as the related angle of 220°?
Because the angle lies between the x-axis, which is the 180° landmark, and ends at the 220° mark, all we did was find the difference between those two degrees. We all know how to do that now, don't we? Simply subtract 180° from 220°, and therefore, we get 40°. Calculating the related angles of letters b and c are done the same way. To me, it's easier to understand when I draw a diagram of it.
(sorry my coloring looks weird!)
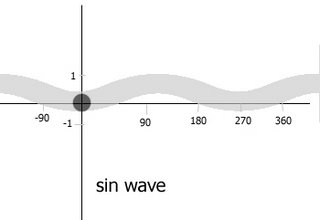
Mr. K also discussed with the class about the Cartisan plane. He mentioned that sin values lie on the y-axis and the cos values lie on the x-axis.
Concerning angles and related angles, he told us that as an angle gets bigger on the plane, the sin value becomes greater -- it eventually reaches a maximum of 1, and 90°. As it passes 90°, it'll begin to back down to 180°.
Remember that if the angle goes past 180°, and is underneath the x-axis, the angle becomes negative, and will have a minimum value.
A diagram can explain what's mentioned above.
On another note, on the Cartisan Plane, if your cos Θ is negative, your angle will lay on the x-axis, in either quads 2 or 3. However if your cos Θ is positive, it will lay in either quads 1 or 4.
If your sin Θ is positive, your angle will lay on the y-axis, in either quads 1 or 2. Otherwise, if your sin Θ is negative, it will lay in quads 3 or 4.
"Mathematics is the science of patterns"
That's what Mr. K has taught us. We also were asked to solve for x in the following equations:
a) 2x + 1 = 0
2x = -1
x = -1/2
b) 2x² - x - 1 = 0
(2x + 1)(x - 1)
x = -1/2
x = 1
c) 3x - 4 = 7x + 2
-6 = 4x
x = -3/2
Mr. K decided to re-write these equations and replace the x's for sin Θ and cos Θ.
We re-wrote them, and we did get the same answers for all of them. This means that renaming the variable into sin Θ and cos Θ doesn't make a difference, but Mr. K said we'd have to take one extra step into solving the equation -- we'd have to figure out what Θ equals.
*************************************************************
I gave it a shot, and I hope you guys understood my scribe. I'm sorry for the late post, I had volleyball practice til 8:45 pm, and I'm pooped :.
REMINDER: EXERCISE 9 WAS FOR HOMEWORK.
And the moment you've all been waiting for.
The next scribe will be m@rk!
goodnight!

Cherrie!
ReplyDeleteyour diagrams are awesome!. =D